Factors Affecting Option Prices

• There are six factors affecting the price of a stock option:
  1. The current stock price,
  2. The strike price, K
  3. The time to expiration, T
  4. The volatility of the stock price,
  5. The risk-free interest rate, r
  6. The dividends that are expected to be paid.

• The effects of the 6 factors are summarized in this table.

Variable	European Call	European Put	American Call	American Put
Current Stock Price
Strike Price
Time of Expiration
Volatility
Risk-free Rate
Amount of future dividends

Factors Affecting Option Prices – Stock Price

• If a call option is exercised at some future time, the payoff will be the amount by which the stock price exceeds the strike price. Call options therefore become more valuable as the stock price increases.
• For a put option, the payoff on exercise is the amount by which the strike price exceeds the stock price. Put options therefore behave in the opposite way from call options: they become less valuable as the stock price increases.

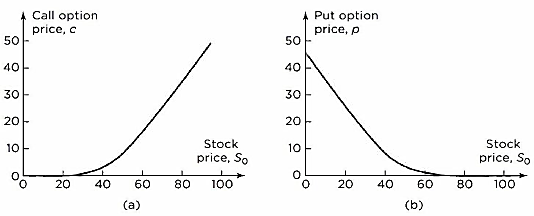
• This figure shows how European call and put prices depend on the Strike Price (K) in the situation where S₀ = 50, K = 50, r = 5% per annum, σ = 30% per annum, T = 1 year, and there are no dividends. In this case, the call price is 7.116 and the put price is 4.677.

• If a call option is exercised at some future time, the payoff will be the amount by which the stock price exceeds the strike price. Call options therefore become less valuable as the strike price increases.
• For a put option, the payoff on exercise is the amount by which the strike price exceeds the stock price. Put options therefore behave in the opposite way from call options: they become more valuable as the strike price increases.

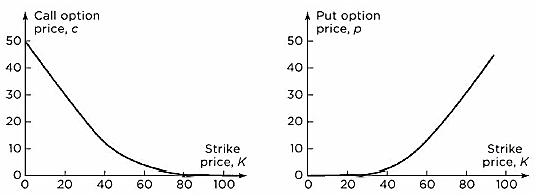
• This figure shows how European call and put prices depend on the Strike Price (K) in the situation where S₀ = 50, R = 50, r = 5% per annum, per annum, T = 1 year, and there are no dividends. In this case, the call price is 7.116 and the put price is 4.677.

Factors Affecting Option Prices – Time To Expiration

• Both put and call American options for non-dividend-paying stocks become more valuable (or at least do not decrease in value) as the time to expiration increases. Consider two American options that differ only as far as the expiration date is concerned. The owner of the long-life option has all the exercise opportunities open to the owner of the short-life option-and more. The long-life option must therefore always be worth at least as much as the short-life option.

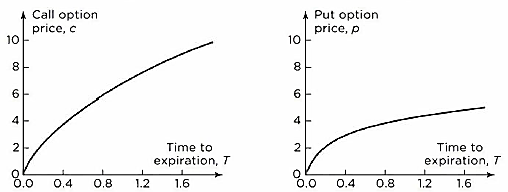
• This figure shows how European call and put prices depend on the Time to Expiration (T) in the situation where S₀ = 50, K = 50, r = 5% per annum, per annum, T = 1 year, and there are no dividends. In this case, the call price is 7.116 and the put price is 4.677.
• For dividend-paying stocks, this is not always the case. Consider two European call options on a stock: one with an expiration date in 1 month, the other with an expiration date in 2 months. Suppose that a very large dividend is expected in 6 weeks. The dividend will cause the stock price to decline, so that the short-life option could be worth more than the long-life option.

Factors Affecting Option Prices – Volatility

• Roughly speaking, the volatility of a stock price is a measure of how uncertain we are about future stock price movements. As volatility increases, the chance that the stock will do very well or very poorly increases. For the owner of a stock, these two outcomes tend to offset each other. However, this is not so for the owner of a call or put. The owner of a call benefits from price increases but has limited downside risk in the event of price decreases because the most the owner can lose is the price of the option. Similarly, the owner of a put benefits from price decreases but has limited downside risk in the event of price increases. The values of both calls and puts therefore increase as volatility increases.

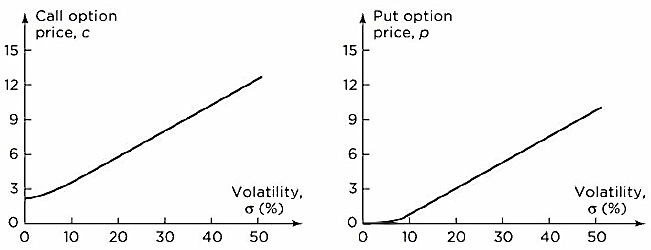
• This figure shows how European call and put prices depend on the Volatility in the situation where S₀, K = 50, r = 5% per annum, per annum, T= 1 year, and there are no dividends. In this case, the call price is 7.116 and the put price is 4.677.

Factors Affecting Option Prices – Risk-Free Rate

• The risk-free interest rate affects the price of an option in a less clear-cut way. As interest rates in the economy increase, the expected return required by investors from the stock tends to increase. In addition, the present value of any future cash flow received by the holder of the option decreases. The combined impact of these two effects is to increase the value of call options and decrease the value of put options.

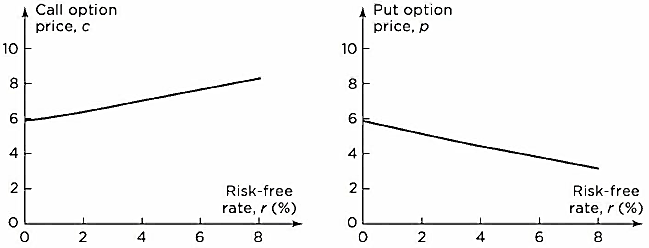
• This figure shows how European call and put prices depend on the Risk-free Rate (r) in the situation where , K = 50, r = 5% per annum, per annum, T = 1 year, and there are no dividends. In this case, the call price is 7.116 and the put price is 4.677.
• It is important to emphasize that we are assuming that interest rates change while all other variables, including the stock price, stay the same. In practice, when interest rates rise (fall), stock prices tend to fall (rise). The combined effect of an interest rate increase and the accompanying stock price decrease can be to decrease the value of a call option and increase the value of a put option. Similarly, the combined effect of an interest rate decrease and the accompanying stock price increase can be to increase the value of a call option and decrease the value of a put option.

Factors Affecting Option Prices – Dividends

• Dividends have the effect of reducing the stock price on the ex-dividend date. This is bad news for the value of call options and good news for the value of put options. Consider a dividend whose ex-dividend date is during the life of an option. The value of the option is negatively related to the size of the dividend if the option is a call and positively related to the size of the dividend if the option is a put.

Assumptions And Notation

• For this chapter, it is to be assumed that there are some market participants, such as large investment banks, for which the following statements are true:

1. There are no transaction costs.
2. All trading profits (net of trading losses) are subject to the same tax rate.
3. Borrowing and lending are possible at the risk-free interest rate.
4. Market participants are prepared to take advantage of arbitrage opportunities as they arise, so that any available arbitrage opportunities disappear very quickly and they are not present in the market.

• The following notation will be used
  • : Current stock price
  • C: Value of American call option to buy one share
  • K: Strike price of option
  • P: Value of American put option to sell one share
  • T: Time to expiration of option
  • c: Value of European call option to buy one share
  • S_T: Stock price on the expiration date
  • p: Value of European put option to sell one share
  • r: Continuously compounded risk-free rate of interest for an investment maturing in time T

Upper Bounds For Option Prices

• An American or European call option gives the holder the right to buy one share of a stock for a certain price. No matter what happens, the option can never be worth more than the stock.

Hence, the stock price is an upper bound to the option price:

and

If these relationships were not true, an arbitrageur could easily make a riskless profit by buying the stock and selling the call option.

• An American put option gives the holder the right to sell one share of a stock for K. No matter how low the stock price becomes, the option can never be worth more than K. Hence,

For European options, we know that at maturity the option cannot be worth more than K. It follows that it cannot be worth more than the present value of K today:

If this were not true, an arbitrageur could make a riskless profit by writing the option and investing the proceeds of the sale at the risk-free interest rate.

Lower Bounds For Call Option Prices

• A lower bound for the price of a European call option on a non-dividend-paying stock is

Example – Suppose that , K = $18, r = 10% per annum, and T = 1 year.

In this case,

Consider the situation where the European call price is $3.00, which is less than the theoretical minimum of $3.71. An arbitrageur can short the stock and buy the call to provide a cash

inflow of $20.00 – $3.00 = $17.00. If invested for 1 year at 10% per annum, the $17.00

grows to . At the end of the year, the option expires. If the stock price is

greater than $18.00, the arbitrageur exercises the option paying $18.00 for the stock and uses the stock to close out the short position. This leads to a profit of

$18.79 – $18.00 = $0.79

If the stock price is less than $18.00, the stock is bought in the market and the short position is closed out. The arbitrageur then makes an even greater profit. For example, if the stock price is $17.00, the arbitrageur’s profit is

$18.79 – $17.00 = $1.79

• For a more formal argument, let’s consider the following two portfolios:
  • Portfolio A: one European call option plus a zero-coupon bond that provides a payoff of K at time T.
  • Portfolio B: one share of the stock.

In portfolio A, the zero-coupon bond will be worth K at time T.

If , the call option is exercised at maturity and portfolio A is worth .

If , the call option expires worthless and the portfolio is worth K. Hence, at time T, portfolio A is worth

Portfolio B is worth ST at time T. Hence, portfolio A is always worth as much as, and can be worth more than, portfolio B at the option’s maturity. It follows that in the absence of arbitrage opportunities this must also be true today. The zero-coupon bond is worth today. Hence,

Because the worst that can happen to a call option is that it expires worthless, its value cannot be negative. This means that c ≥ 0 and so that

Lower Bounds For Call Option Prices – Example

• Consider a European call option on a non-dividend-paying stock when the stock price is $51, the strike price is $50, the time to maturity is 6 months, and the risk-free interest rate is 12% per annum. In this case, , K = 50, T = 0.5, and r = 0.12. Find the lower bound for the option price

Lower Bounds For Put Option Prices

• For a European put option on a non-dividend-paying stock, a lower bound for the price is

Example – Suppose that , K = $40, r = 5% per annum, and T = 0.5 years.

In this case,

Consider the situation where the European put price is $1.00, which is less than the theoretical minimum of $2.01. An arbitrageur can borrow $38.00 for 6 months to buy both the put and the stock. At the end of the 6 months, the arbitrageur will be required to repay . If the stock price is below $40.00, the arbitrageur exercises the option to sell the stock for $40.00, repays the loan, and makes a profit of

$40.00 – $38.96 = $1.04

If the stock price is greater than $40.00, the arbitrageur discards the option, sells the stock, and repays the loan for an even greater profit. For example, if the stock price is $42.00, the arbitrageur’s profit is

$42.00 – $38.96 = $3.04

• For a more formal argument, let’s consider the following two portfolios:
  • Portfolio C: one European put option plus one share.
  • Portfolio D: a zero-coupon bond paying off K at time T.

If , then the option in portfolio C is exercised at option maturity and the portfolio becomes worth K.

If , then the put option expires worthless and the portfolio is worth at this time.

Hence, portfolio C is worth in time T.

Portfolio D is worth K in time T. Hence, portfolio C is always worth as much as, and can sometimes be worth more than, portfolio D in time T. It follows that in the absence of arbitrage opportunities portfolio C must be worth at least as much as portfolio D today.

Hence,

Because the worst that can happen to a put option is that it expires worthless, its value cannot be negative. This means that

Lower Bounds For Put Option Prices – Example

• Consider a European put option on a non-dividend-paying stock when the stock price is $38, the strike price is $40, the time to maturity is 3 months, and the risk-free rate of interest is 10% per annum. In this case, , K = 40, T = 0.25, and r = 0.10. Find the lower bound for the option price.

Put-Call Parity

• This is an important relationship between the prices of European put and call options that have the same strike price and time to maturity. Consider two portfolios from the previous section:
  • Portfolio A: one European call option plus a zero-coupon bond that provides a payoff of K at time T.
  • Portfolio C: one European put option plus one share of the stock.

The call and put options have the same strike price K and the same time to maturity T.

As discussed in the previous section, the zero-coupon bond in portfolio A will be worth K at time T. If the stock price at time I proves to be above K, then the call option in portfolio A will be exercised. This means that portfolio A is worth at time T in these circumstances. If St proves to be less than K, then the call option in portfolio A will expire worthless and the portfolio will be worth K at time T.

In portfolio C, the share will be worth at time T. If St proves to be below K, then the put option in portfolio C will be exercised. This means that portfolio C is worth at time I in these circumstances. If St proves to be greater than K, then the put option in portfolio C will expire worthless and the portfolio will be worth St at time T.

• The situation is summarized in the table.

Portfolio	Constituents
	Call option
	Zero-coupon bond
	Total
	Put Option
	Share
	Total

If , both portfolios are worth at time T; if , both portfolios are worth K at time T. In other words, both are worth

when the options expire at time T.

Because they are European, the options cannot be exercised prior to time T.

Since the portfolios have identical values at time T, they must have identical values today. If this were not the case, an arbitrageur could buy the less expensive portfolio and sell the more expensive one. The constituents of portfolio A are worth c and today, and the components of portfolio C are worth p and So today. Hence,

This relationship is known as put-call parity. It shows that the value of a European call with a certain exercise price and exercise date can be deduced from the value of a European put with the same exercise price and exercise date, and vice versa.

Put-Call Parity – Layman Example

• Consider the Pay-off of a trader who has the following position:
  • A Call Option with a Strike Price of 5 and
  • A Bond with a maturity value of 5.

			Portfolio Payoff (Call + Bond)
0
1
2
3
4			</td >
5
6
7
8
9
10

• Consider, now, the Pay-off of a trader who has:
  • A Put Option with a Strike Price of 5 and
  • An equivalent unit of the underlying asset.

			Portfolio Payoff (Put + Stock)
0
1
2
3
4
5
6
7
8
9
10

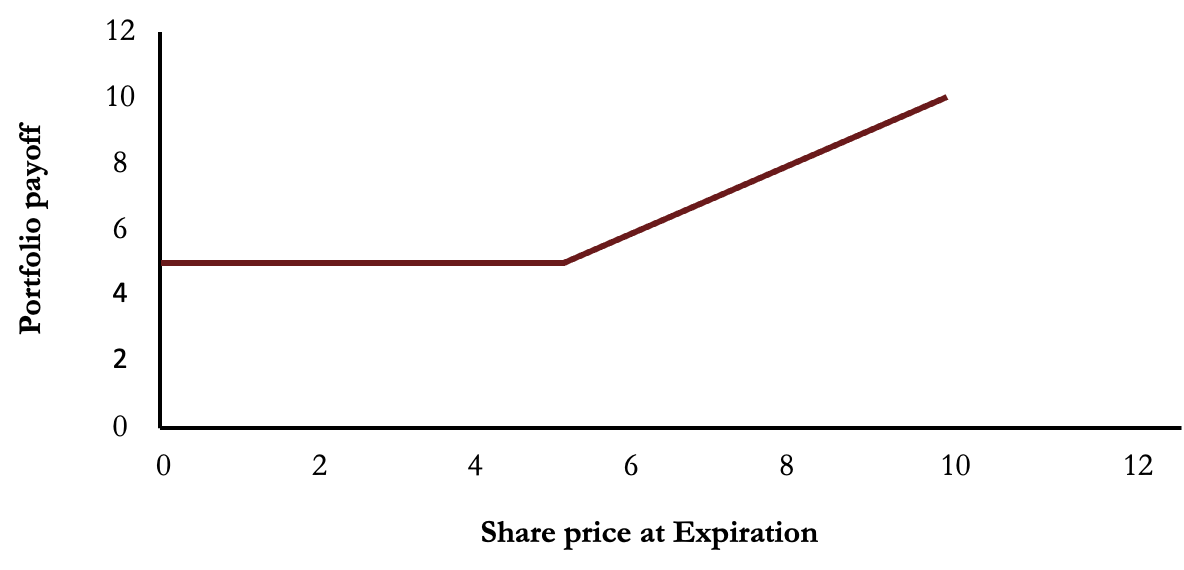
• The payoff for both the portfolios are the same represented by this graph

Put-Call Parity And American Options

• Put-call parity holds only for European options. However, it is possible to derive some results for American option prices. It can be shown that, when there are no dividends,

Example

An American call option on a non-dividend-paying stock with strike price $20.00 and maturity in 5 months is worth $1.50. Suppose that the current stock price is $19.00 and the risk-free interest rate is 10% per annum. From the above inequality

or

showing that P – C lies between $1.00 and $0.18. If C is $1.50, P must lie between $1.68 and $2.50. In other words, upper and lower bounds for the price of an American put with the same strike price and expiration date as the American call are $2.50 and $1.68.

American Calls On A Non-Dividend-Paying Stock

• It can be shown that it is never optimal to exercise an American call option on a non-dividend paying stock before the expiration date.

Consider an American call option on a non-dividend-paying stock with one month to expiration when the stock price is $70 and the strike price is $40. The option is deep in the money, and the investor who owns the option might well be tempted to exercise it immediately.

However, if the investor plans to hold the stock obtained by exercising the option for more than one month, this is not the best strategy. A better course of action is to keep the option and exercise it at the end of the month. The $40 strike price is then paid out one month later than it would be if the option were exercised immediately, so that interest is earned on the $40 for one month. Because the stock pays no dividends, no income from the stock is sacrificed. A further advantage of waiting rather than exercising immediately is that there is some chance (however remote) that the stock price will fall below $40 in one month. In this case the investor will not exercise in one month and will be glad that the decision to exercise early was not taken!

This argument shows that there are no advantages to exercising early if the investor plans to keep the stock for the remaining life of the option (one month, in this case).

• Even if the investor thinks the stock is currently overpriced and is planning to exercise the option and sell the stock, the investor would be better off selling the option than exercising it. The option will be bought by another investor who does want to hold the stock. Such investors must exist. Otherwise the current stock price would not be $70. The price obtained for the option will be greater than its intrinsic value of $30, for the reasons mentioned earlier.
• To summarize, there are two reasons an American call on a non-dividend-paying stock should not be exercised early.
  • One relates to the insurance that it provides. A call option, when held instead of the stock itself, in effect insures the holder against the stock price falling below the strike price. Once the option has been exercised and the strike price has been exchanged for the stock price, this insurance vanishes.
  • The other reason concerns the time value of money. From the perspective of the option holder, the later the strike price is paid out the better.

Bounds On American Calls On A Non-Dividend-Paying Stock

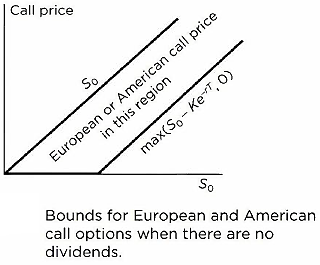
• Because American call options are never exercised early when there are no dividends, they are equivalent to European call options, so that C = c.
  • Hence, it follows that lower bounds for both c and C is given by
  • Also, it follows that upper bounds for both c and C is given by

These bounds are illustrated in this figure

American Calls On A Non-Dividend-Paying Stock

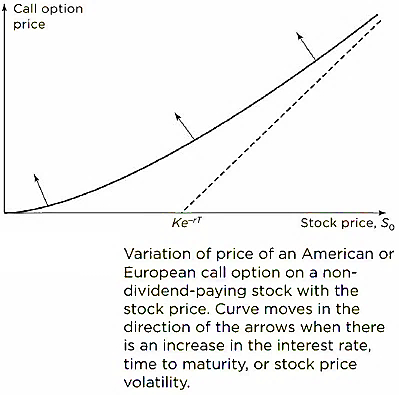
• The general way in which the call price varies with the stock price, , is shown in this figure. As r or T or the stock price volatility increases, the line relating the call price to the stock price moves in the direction indicated by the arrows.

• It can be optimal to exercise an American put option on a non-dividend-paying stock early. Indeed, at any given time during its life, the put option should always be exercised early if it is sufficiently deep in the money. To illustrate, consider an extreme situation. Suppose that the strike price is $10 and the stock price is virtually zero. By exercising immediately, an investor makes an immediate gain of $10. If the investor waits, the gain from exercise might be less than $10, but it cannot be more than $10, because negative stock prices are impossible. Furthermore, receiving $10 now is preferable to receiving $10 in the future. It follows that the option should be exercised immediately.
• Like a call option, a put option can be viewed as providing insurance. A put option, when held in conjunction with the stock, insures the holder against the stock price falling below a certain level. However, a put option is different from a call option in that it may be optimal for an investor to forgo this insurance and exercise early in order to realize the strike price immediately.
• In general, the early exercise of a put option becomes more attractive as So decreases, as r increases, and as the volatility decreases.

Bounds On American Puts On A Non-Dividend-Paying Stock

• • The lower and upper bounds for a European put option when there are no dividends are given by
    For an American put option on a non-dividend-paying stock, the condition

must apply because the option can be exercised at any time. This is a stronger condition than the one for a European put option

• • Hence, it follows that lower bounds for P is given by
  • Also, it follows that upper bounds for P is given by K

This figure illustrates the bounds

Puts On A Non-Dividend-Paying Stock

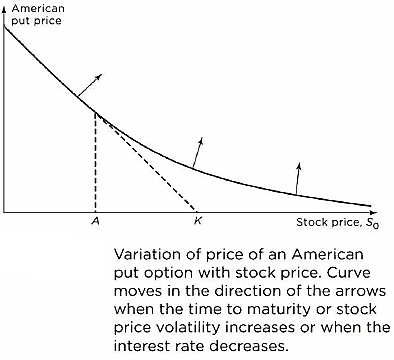
• This figure shows the general way in which the price of an American put option varies with So. If r > 0, it is always optimal to exercise an American put immediately when the stock price is sufficiently low. When early exercise is optimal, the value of the option is . The curve representing the value of the put therefore merges into the put’s intrinsic value, , for a sufficiently small value of So. In this figure, this value of So is shown as point A. The line relating the put price to the stock price moves in the direction indicated by the arrows when r decreases, when the volatility increases, and when T increases.

• Because there are some circumstances when it is desirable to exercise an American put option early, it follows that an American put option is always worth more than the corresponding European put option. Furthermore, because an American put is sometimes worth its intrinsic value, it follows that a European put option must sometimes be worth less than its intrinsic value. This means that the curve representing the relationship between the put price and the stock price for a European option must be below the corresponding curve for an American option.
• This figure shows the variation of the European put price with the stock price. Point B in this figure, at which the price of the option is equal to its intrinsic value, must represent a higher value of the stock price than point A in the previous figure because the curve in this figure is below the curve in the previous figure. Point E in this figure is where and the European put price is .

Effect Of Dividends

• The results produced so far in this chapter have assumed that we are dealing with options on a non-dividend-paying stock. This section examines the impact of dividends. It is assumed that the dividends that will be paid during the life of the option are known. In many situations, this assumption is often not too unreasonable. PV (D) will be used to denote the present value of the dividends during the life of the option. In the calculation of PV (D), a dividend is assumed to occur at the time of its ex-dividend date.
• The analysis that has been carried out before can be done in the same way by redefining Portfolios A, B, C, and D as follows:
  • Portfolio A: one European call option plus an amount of cash equal to
  • Portfolio B: one share
  • Portfolio C: one European put option plus one share
  • Portfolio D: an amount of cash equal to

Effect Of Dividends On Bounds And Early Exercise

• Lower bound for call becomes

• Lower bound for put becomes

• Early Exercise

When dividends are expected, it can no longer be asserted that an American call option will not be exercised early. Sometimes it is optimal to exercise an American call immediately prior to an ex-dividend date. It is never optimal to exercise a call at other times.

Effect Of Dividends On Put-Call Parity

• Comparing the value at option maturity of the redefined portfolios A and C shows that, with dividends, the put-call parity result becomes

• For American call, the inequality changes to