Introduction

• Some important metrics in the analysis of fixed-income portfolios are:
  • DV01
  • Duration
  • Convexity

• These are one-factor risk metrics (i.e., they are based on the assumption that interest rate term structure movements are driven by a single factor).
• The yield-based measures of duration and convexity consider what happens to a bond price when there is a small change to its yield. Effective duration and effective convexity consider what happens when all spot rates change by the same amount i.e. for a parallel change in the yield curve.
• The measures considered in this chapter only quantify the impact of a parallel shift in the interest rate term structure. DV01 and duration describe what happens when there is a small parallel shift in the term structure. Convexity extends the duration analysis to larger parallel shifts. Hedging strategies based on these measures work well for parallel term structure shifts. However, they are liable to be less effective for non-parallel shifts.

The One Factor Assumption

• The simplest one-factor model assumes that all interest rates move by the same amount. Under this simple model, the shape of the term structure never changes. If the three-year spot rate increases by five basis points, all other spot rates increase by five basis points. If the three-year spot rate decreases by one basis point, all other spot rates decrease by one basis point. This model is illustrated by this Figure.

• In this model, the movement of one interest rate over a short period of time can be used to determine the movement of all interest rates during that period.
• One-factor term structure shifts do not need to be parallel. In fact, some proposed one-factor models lead to long-maturity rates moving by less than short-maturity rates. For example, a particular model might predict that when the one-year rate increases by ten basis points during a short period, the three-year rate increases by seven basis points and the ten-year rate increases by only four basis points. This type of model is illustrated in this Figure. This is still a one-factor model because the movement in all points over a short period can be calculated when the movement in one rate is known.
• The term structure shape can be upward or downward sloping in a one factor model.

DV01

• DV01 describes the impact of a one-basis-point change in interest rates on the value of a portfolio.

where

∆r is the size of a parallel shift in the interest rate term structure (measured in basis points), and

∆P is the resultant change in the value (P) of the position being considered.

For a long position in a bond, DV01 is positive because a bond price is negatively correlated to interest rate changes. The bond price increases (decreases) when rates decrease (increase).

EXAMPLE

• Suppose a portfolio consists of a three-year Treasury bond with a face value of USD 1 million paying a 10% per annum coupon semi-annually. Suppose further that spot rates are as shown in this Table. The value of the bond, assuming no spread, is
• If rates increase by five basis points (i.e., by 0.05%), the six-month rate
  becomes 7.05%, the one-year rate becomes 7.55%, and so on. The value of the bond is then:

Maturity (Years)	Rate (%)
0.5	7.0
1.0	7.5
1.5	8.0
2.0	8.3
2.5	8.5
3.0	8.6

• A five-basis-point increase in all rates causes the bond price to decline by

DV01 can be calculated as

• Now suppose rates decrease by five basis points per year. The six-month rate becomes 6.95%, the one-year rate becomes 7.45%, and so on. The value of the bond become

A five-basis-point decrease in rates causes the bond price to increase by

DV01 can be calculated as

These results can be summarized in this Table

Change	New Bond Price (USD)	Increase in Bond Price (USD)	DV01 Estimate
Five-basis point increase of all rates	1,036,594.522	-1327.510	265.502
Five-basis-point decrease in all rates	1,039,251.681	1329.649	265.9298

• The two estimates of DV01 differ slightly because the bond’s price is not exactly a linear function of interest rates. A good estimate of DV01 can be obtained by averaging the two estimates:

• In this definition of DV01, it has been assumed all spot rates increase by one basis point.  A slightly different definition of DV01 can be obtained if it is assumed that the bond yield increases by one basis point. Yet another possible definition of DV01 is obtained by increasing forward rates by one basis point. The result is again very similar to (but not quite the same as) increasing all spot rates by one basis point. Some analysts distinguish between these definitions as follows.
  • Yield-based DV01: The change in price from a one-basis-point increase in a bond’s yield.
  • DVDZ or DPDZ: The change in price from a one-basis-point increase in all spot (i.e., zero) rates.
  • DVDF or DPDF: The change in price from a one-basis-point increase in forward rates.

In this chapter, it will assumed that DV01 is calculated from a one-basis-point change in all spot rates (i.e., a one-basis-point parallel shift in the term structure of spot rates).

DV01 And Hedging

• DV01 can be calculated for any position whose value depends on interest rates. For example, suppose that the DV01 for a bank’s position (in USD per basis point) is -463. This means the position gains value when interest rates increase and loses value when interest rates decrease. Specifically:
  • If all rates increase by one basis point, the value of the bank’s position increases by USD 463, and
  • If all rates decrease by one basis point, the value of the bank’s position decreases by USD 463.
• The bank’s position can be hedged with the 10% coupon bond that was considered earlier.

Effective Duration

• DV01 is the decrease (increase) in the price of a bond (or other instrument) arising from a one-basis-point increase (decrease) in rates. When the instrument is a bond, ∆P/∆r is negative so that DV01 is positive. While DV01 measures an actual change in price, effective duration describes the percentage change in the price of a bond (or other instrument) due to a small change in all rates. Denoting the effective duration of an instrument by D and the change in rates by ∆r,

⇒∆P=-DP∆r

Effective duration can also be written in the instantaneous form as

• When the change in rates is measured in basis points, effective duration is DV01 divided by the price of the bond.

⇒D=DV01/P

In the case of the bond considered earlier,

This is the proportional change in the price of the instrument due to a one-basis-point change in all interest rates. In this case, the effective duration is 0.0256%.

Effective Duration – Callable And Putable Bonds

• A callable bond is a bond where the issuing company has the right to buy back the bond at a pre-determined price at certain times in the future. A company will tend to do this when interest rates have declined so that it can re-finance at a lower rate.
• Consider a five-year bond that can be called after three years (but not at any other time).
  • An approach to calculate effective duration can be to ignore the call feature and regard the bond as a non-callable five-year bond. This is an incorrect assumption because the call feature reduces duration.
  • Another approach would be to assume that the probability of the bond being called remains constant. For example, suppose that when the bond is valued there is a 40% chance that the bond will be called. When calculating the effective duration, the following can be calculated –

: the effective duration of the three-year bond,

: the effective duration of the five-year bond

• Then the effective duration of the callable bond can be set as:
  • Although this approach is better than ignoring the call feature, it would not be correct either. When interest rates increase, the probability of the bond being called is reduced. A correct approach is therefore as follows:
    • Value the bond today.
    • Value the bond if all interest rates increase by one basis point. (This calculation incorporates the effect of the one-basis-point increase on the probability of the bond being called.)
    • Calculate effective duration from the percentage change in the price.
• A putable bond is a bond where the holder has the right to demand early repayment. A putable bond should be treated like a callable bond when calculating effective duration. In this case, the probability of the put option being exercised increases as interest rates increase.

Effective Duration Versus DV01

• In choosing between effective duration and DV01,
  • DV01 is appropriate to consider the impact of rate changes on the value of a position in dollars.
  • Effective duration is appropriate to consider the impact of rate changes on the value of a position as a percentage.

• DV01 increases as the size of a position increases, while effective duration does not. (If a position is doubled in size, DV01 doubles while effective duration remains the same.)

• A bond investor is usually interested in returns, which are typically measured in percentage terms. This usually means effective duration is the better measure. However, DV01 is likely to be the most appropriate measure for swaps (as well as interest rate futures).

Effective Convexity

• Effective convexity measures the sensitivity of the duration measure to changes in interest rates. The effective convexity (C) of a position worth P can be estimated as:

where

is the value of the position when all rates increase by ∆r and

is the value of a position when all rates decrease by ∆r.

∆r is measured as a decimal.

EXAMPLE

• Consider again the bond discussed earlier. This is a three-year bond paying a coupon of 10% per year semi-annually.

P= 1,037,922.032

The estimate of convexity is

Convexity – Impact Of Parallel Shifts

• Effective duration provides the impact of a small parallel shift in the term structure. However, consider again the bond discussed earlier valued at USD 1,037,922.03. If rates increase by 20 basis points, the term structure is as shown in this Table:

The value of the bond (USD) is

The bond’s price decreases by

1, 037,922.032 – 1,032, 624.792 = 5297.24

∆P=-5297.24

The duration relation predicts a price change of:

∆P = -DP∆r = -0.000256 x 1,037,922.032 x 20 = -5314.16

This is reasonably accurate, but it can be made more accurate using the convexity (C).

Maturity (Years)	Rate (%)
0.5	7.2
1.0	7.7
1.5	8.2
2.0	8.5
2.5	8.7
3.0	8.8

• The estimate of the price change using both duration and convexity is

This is very close to the price decrease of  5297.24 that was calculated by revaluing the bond.

• The accuracy of the estimate using effective duration declines with the size of the parallel shift considered. However, the duration + convexity approximation can give a reasonable answer even for quite large changes.

Convexity

• The effective duration approximation for a bond is illustrated in this Figure. Actually, there is a non-linear relationship between ∆P/P and ∆r. Effective duration approximates this as a linear relation because it is the gradient of the curve relating ∆P/P and ∆r at the origin. The linear approximation provided by duration becomes less accurate as the (positive or negative) magnitude of ∆r increases. The duration plus convexity approximation fits a quadratic function and captures some of the curvature. As a result, it provides a better approximation.

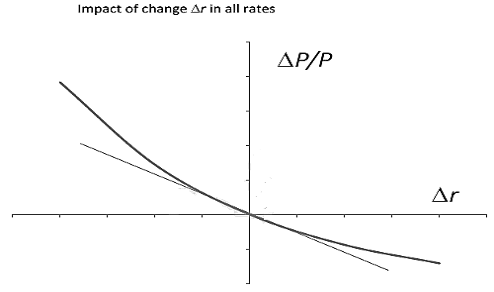
• One important point illustrated by the previous Figure is that the actual percentage change in a bond price is always greater than that predicted by duration.
• Duration overestimates the magnitude of price decreases
• Duration underestimates the magnitude of price increases.
• Meanwhile, the convexity measure provides an estimate of the difference between:
  • The bond price change predicted by effective duration, and
  • The actual bond price change.
• This explains why convexity is positive for a long bond position.
• As convexity increases, the curvature of the relationship between bond price changes (measured in percentage terms) and rate changes increases.

Portfolio Calculations

• The DV01 for a portfolio is simply the sum of the DV01s of the components of the portfolio. If a portfolio consists of three positions that have DV01s (in thousands of USD) of 30, 40, and 50 (respectively), the DV01 of the portfolio is 30 + 40 + 50 = 120

• The duration of a portfolio is the average of the durations for the individual instruments within the portfolio weighted by the value of each instrument. For example, consider a portfolio consisting of three bonds worth (in USD millions) 10, 15, and 25. Suppose that the effective durations of the bonds are six, eight, and 11 (respectively). The effective duration of the portfolio is

• Convexity for a portfolio is handled like duration. It is the average of the convexities of the instruments within the portfolio weighted by the value of each instrument.

Barbell Versus Bullet

• Consider three bonds:

1. A 5–year bond with a 2% coupon,
2. A 10–year bond with a 4% coupon, and
3. A 20–year bond with a 6% coupon.

It is assumed that the term structure of interest rates is flat at 4% (semi-annually compounded). The effective durations and convexities of the three bonds are shown in this Table

Bond	Value	Effective Duration	Effective Convexity
5-year, 2% coupon	91.0714	4.6764	24.8208
10-year, 4% coupon	100.0000	8.1758	78.8981
20-year, 6% coupon	127.3555	12.6235	212.4604

If an investor wants a portfolio with an effective duration of 8.1758, he or she can buy the ten-year, 4% coupon bonds. This is referred to as a bullet investment because only one bond is involved. An alternative is to construct a portfolio from the other two bonds with an effective duration equal to 8.1758. This is known as a barbell investment. Suppose that a proportion β of the portfolio is invested in the five-year bond, and a proportion (1-β) is invested in the 20-year bond. The duration will be

There are therefore two ways a portfolio with a duration of 8.1758 can be created

• Invest all funds in the ten-year, 4% coupon bond, or
• Invest  56% of funds in the five-year, 2% coupon bond and 44% of the funds in the 20-year, 6% coupon bond.

The portfolios have the same duration but different convexities. The first has a convexity of 78.8981. The second alternative has a convexity of:

24.8208×0.56+212.4604×0.44=107.382

A higher convexity improves the bond holder’s position when there is a parallel shift in interest rates. As convexity increases, the improvement increases.

While both strategies provide a yield of 4% and a duration of 8.1758, the barbell strategy always produces a better result when there is a parallel shift in the yield curve. The barbell strategy therefore appears to dominate the bullet strategy.