Introduction

• Standard European and American options (i.e., those usually traded on exchanges) are termed plain vanilla options.
• Options with non-standard properties are termed exotic options (or simply exotics). These exotics are designed by derivatives dealers to meet the specific needs of their clients and are usually traded in the over-the-counter markets.
• Exotic options can be very profitable for derivatives dealers because they have relatively large bid-offer spreads.
• Exotic options arise for several reasons.
  • In some situations, they can provide more efficient hedging than plain vanilla options.
  • Exotic options may also best reflect a firm’s view on factors such as interest rates, exchange rates, and commodity prices.
  • Occasionally, exotic options are used for tax or regulatory purposes.

Packages

• A package is a portfolio consisting of plain vanilla options on an asset. Several packages have been discussed earlier like
  • bull spreads,
  • bear spreads,
  • butterfly spreads,
  • calendar spreads,
  • straddles, and
  • strangles.
• Packages are sometimes regarded as exotic options because they are positions built to reflect a specific market view and risk tolerance. For example, an investor who takes a long position in a butterfly spread is acting on his or her belief that the future asset price will be near the middle strike price. At the same time, the investor is building this position without taking on a great deal of risk. In contrast, an investor with a similar view of the market who chooses to sell a straddle or a strangle is taking on much more risk.

Zero Cost Products

• Since packages generally involve selling one instrument and buying another, they can be designed by derivatives dealers so that it will have zero cost initially. This can be done if the premium paid for a long position is equal to the premium received for short positions, resulting in a construction whose initial cost is zero to the investor.
• Apart from this, any derivative product can also be converted into a zero-cost product by arranging for it to be paid for in arrears –
  • Consider a derivative that matures at time T and has a premium equal to f. Rather than requiring that the premium be paid upfront (which is normally the case), the derivative can be structured so that the buyer instead pays
    at maturity, which is the future value of the premium (where R is the interest rate for maturity T).
  • For a practical example, consider a European call option with premium c. The option buyer will pay an amount equal to the future value of c, which is . Hence, when converted into a zero-cost product, it has a profit equal to payoff minus premium which is:

In essence, this is a forward contract where the holder agrees to buy the option payoff at maturity for A.

• • One extension of the above idea is to make the zero-cost product a futures contract (rather than a forward contract) on the option payoff. This is known as a futures-style option. For example, a futures-style call is marked to market in the same way as a regular futures contract with the final settlement of
    , where is the final price of the underlying asset and K is the strike price. Futures-style options are offered by exchanges such as the CME Group and Eurex. Futures-style options can be contrasted with the more usual equity-style options, which involve the buyer paying an upfront premium.

Non Standard American Options

• Exchange-traded American options can be exercised at any time at the pre-determined fixed strike price. Variations on this standard product are traded in the over-the-counter markets. The following are examples.
  • The exercise may be restricted to certain dates. Such an option is known as a Bermudan option. Interest rate options are sometimes Bermudan (e.g., an American-style bond option might only be exercisable on interest payment dates).
  • There may be an initial lock-out period during which time the option cannot be exercised. As we saw in an earlier chapter, employee stock options usually have a lock-out period. Once the lock-out period is over, employee stock options are referred to as vested.
  • The strike price may change during the life of the option. For example, when a corporate bond has a call option feature allowing the issuer to retire the bond early (i.e., buy it back from the holder), the strike price at which the issuer can exercise the option tends to decline as time passes.
• The binomial tree methodology can be adapted to accommodate all the non-standard features just mentioned.

Nature Of The Underlying

• First, options with payoffs that depend on the prices of only a single asset will be discussed. These include gap, forward start, compound, chooser, barrier, binary, lookback, and Asian options.
• Then, options with payoffs that depend on the prices of two or more assets will be discussed. These include exchange and basket options.
• Some exotic options are dependent on the volatility of an asset price, rather than the asset price itself. These include volatility and variance swaps. These will be discussed after the above.

Gap Options

• A gap option is a European call or put option where the price triggering a payoff is different from the strike price (which is the price used in calculating the payoff). The trigger price may be greater than or less than the strike price. Hence, there is a gap between the trigger price and the strike price.
• Suppose the trigger price is and the strike price is . For a given strike price, the trigger price that produces the maximum gap option price is the strike price.
  • When , the gap option is just like an ordinary option. Gap = 0 in this case.
  • If , then further increase in the value of will lead to the value of the gap option to decrease.
  • If , then further decrease in the value of will also lead to the value of the gap option to decrease.

• In some circumstances, the probability of a negative payoff is sufficiently high such that the cost of a gap option is negative.
• Gap options can be used to describe some insurance contracts.

Gap Call Option

• If , then the gap call option will NOT be exercised and in that case, the payoff from a gap call option is ZERO. If , then the gap call option will BE exercised and in that case, the payoff from a gap call option is

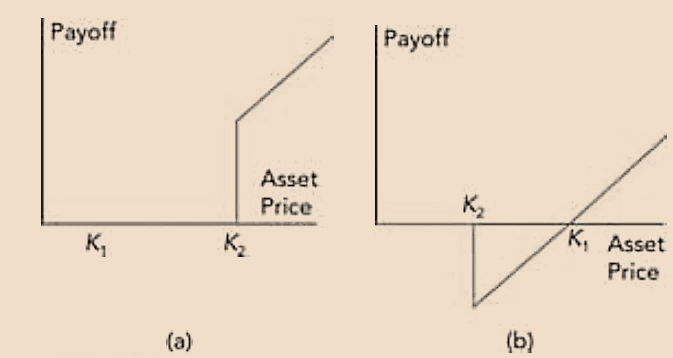
Payoffs from Gap Call Option when (a) and (b)

(a) If

(b) If

And in case (b), the payoff becomes positive once

Gap Put Option

• If , then the gap put option will NOT be exercised and in that case, the payoff from a gap call option is ZERO. If , then the gap put option will BE exercised and in that case, the payoff from a gap call option is

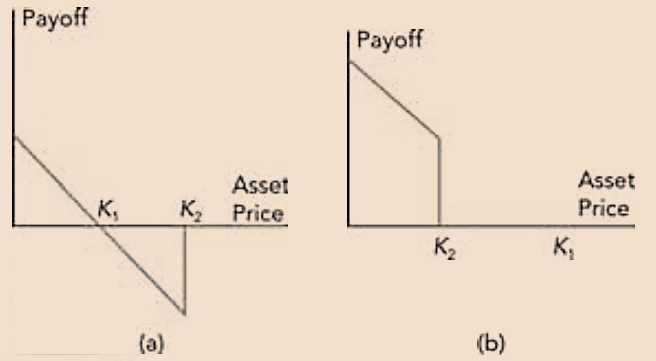
Payoffs from Gap Put Option when (a) and (b)

(a) If

(b) If

Gap Options – Payoffs Summary

• The payoff from a gap call option is

• The payoff from a gap put option is

Range for \(S_T\)	Payoff from Gap Call Option	Payoff from Gap Put Option
\(S_T < K_2\)	0	\(K_1 – S_T\)
\(S_T = K_2\)	\(S_T – K_1\)	\(K_1 – S_T\)
\(S_T > K_2\)	\(S_T – K_1\)	0

Forward Start Options

• A forward start option is an option that will begin at a future time. For example – a 2-year put option which will start to exist 1 year from now.
• It is usually stated that the option will be at-the-money at the time it starts.
• Employee stock options can be forward start options if an employer promises that they will be granted on future dates.
• A series of forward start options is called a cliquet or ratchet option. Thus, a cliquet option comprises of a series of options with a forward start date and certain rules for determining the strike prices. For example, a cliquet option might consist of five call options: a one-year option, a one-year option starting in one year, a one-year option starting in two years, a one-year option starting in three years, and a one-year option starting in four years. This is therefore a portfolio consisting of a regular one-year option plus four forward start options. A simple rule for the strike prices could be that each option is initially at-the-money.
• Cliquet options arise in some annuity contracts.

Compound Options

• A compound option is an option on another option. Thus, there are two strike prices and two maturity dates.
• Suppose the maturity dates are and (with ) and the strike prices corresponding to those maturity dates are and (respectively). Four types of compound options are:

1. Call option on call option – The holder has the right to pay at time in order to obtain a long position in a call option on an asset. This call option allows the asset to be bought for at time .
2. Put option on call option – The holder has the right to receive at time and obtain a short position in a call option on an asset. This call option allows the asset to be bought for at time .
3. Call option on put option – The holder has the right to pay at time in order to obtain a long position in a put option on an asset. This put option allows the asset to be sold for at time .
4. Put option on put option – The holder has the right to receive at time , and obtain a short position in a put option on an asset. This put option allows the asset to be sold for at time .

• Compound options are attractive to traders who want more leverage than that provided by plain vanilla options. For example, suppose that for a non-dividend paying stock is

then

Thus, a compound option (call-on-call) could be structured as follows.

• • At the six-month point, the investor has the right to pay USD 3 for a call option.
  • The call option, if purchased, gives the investor the right to buy the stock for USD 55 at the one-year point.

The BSM assumptions give the value of this compound option as USD 0.99. Assuming no changes in the volatility or the risk-free rate, the BSM model shows that the value of the call option is greater than USD 3 if the stock price at the six-month point is greater than USD 54.30.

The call option will therefore be purchased (i.e. first call on the second call should be exercised) at the six-month point if the stock price is greater than USD 54.30.

• Compared to regular options prices, the prices of compound options are more sensitive to changes in volatility. For example, if σ_annual increases from 20% to 30 % in the previous example, the BSM assumptions show that the price of the compound option in the previous example increases by 160 % (from USD 0.99 to USD 2.57).Meanwhile, using the same assumptions, the price of the regular option increases by only 79% (from USD 2.47 to USD 4.43).

Chooser Options

• With a chooser option, the holder has a period of time (after purchasing the option) where he or she can choose whether it is a put option or a call option. Hence they are sometimes called “as you like it” options. For example, the holder of a two-year European option might be allowed to choose whether it is a call option or a put option at the end of the first year.
• One feature of chooser options is that they can be viewed as packages of call options and put options with different strike prices and times to maturity. To see this, suppose the time when the choice is made is . Assume the value of the chooser option at this time is max(c, p)

where c is the price of a call option, and p is the price of a put option.

This can be rewritten as: c+max(0, p-c)

If both options are European options maturing at time (where ) with strike price K, then from put-call parity –

p – c = PV(K)- S

where PV denotes present value from to . This means that the value of the chooser option is

where

• This above formulation shows that the option is a package consisting of:
  • A call option with strike price K maturing at time , and
  • A put option with strike price PV(K) maturing at time

Barrier Options

• Barrier options have payoffs that depend on whether the asset price reaches a particular barrier. There are four types of barrier options.

1. Down-and-out (d&o) – This is a European (call or put) option that ceases to exist if the asset price moves down from its initial level to the barrier level during the life of the option.
2. Down-and-in (d&i) – This is a European (call or put) option that comes into existence if the asset price moves down from its initial level to the barrier level during the life of the option.
3. Up-and-out (u&o) – This is a European (call or put) option that ceases to exist if the asset price moves up from its initial level to the barrier level during the life of the option.
4. Up-and-in (u&i) – This is a European (call or put) option that comes into existence if the asset price moves up from its initial level to the barrier level during the life of the option.

• Options that cease to exist when a barrier is reached are sometimes referred to as knock-out options, whereas options that come into existence when a barrier is reached are referred to as knock-in options. So 1 & 3 above are knock-out and 2 & 4 are knock-in options. The value of a standard European option can be formulated as the sum of values of knock-out and knock-in options, i.e.

• Barrier options can be attractive to market participants because they are less expensive than regular options.
• Barrier options have some interesting properties. As with binary options and gap options, their payoff is discontinuous. Consider an up-and-out call with a strike price of USD 50 and a barrier at USD 60. If the stock price stays below the barrier and reaches USD 59.90 at maturity, the payoff is USD 9.90. If the stock price is 0.1 higher, the payoff is zero.
• Normally, options prices increase as volatility increases. However, this is not necessarily the case with barrier options. For example, when a knock-out option is close to the barrier, an increase in the volatility may lower the price because it increases the probability that the barrier will be hit.

Binary Options

• There are four types of binary options.

1. Cash-or-nothing call – This pays a fixed amount if the asset price is above the strike price at maturity and zero otherwise.
2. Cash-or-nothing put – This pays a fixed amount if the asset price is below the strike price at maturity and zero otherwise.
3. Asset-or-nothing call – This pays an amount equal to the asset price if it is above the strike price at maturity and zero otherwise.
4. Asset-or-nothing put – This pays an amount equal to the asset price if it is below the strike price at maturity and zero otherwise.

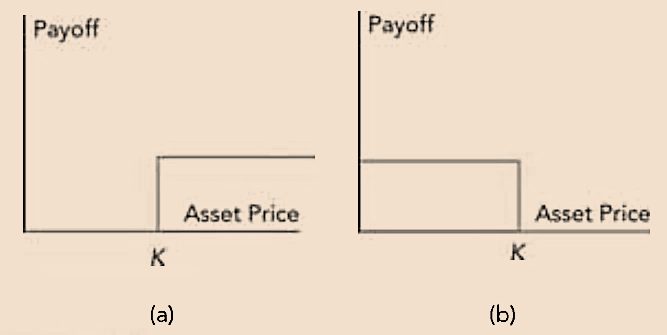
The payoff from (a) a cash-or-nothing call, and (b) a cash-or-nothing put, where K is the strike price.

The payoff from (a) asset or nothing call, and (b) an asset or nothing put, where K is the strike price.

• Traditional European options can be thought of as combinations of binary options.
  • A long position in a European call option is a combination of:
    • A long position in an asset-or-nothing call, and
    • A short position in a cash-or-nothing call with a payoff equal to the strike price.
  • Similarly, a long position in a European put option is
    • A short position in an asset-or-nothing put, and
    • A long position in a cash-or-nothing put with a payoff equal to the strike price.

• Cash-or-nothing options are sometimes referred to as digital options.
• Binary options, like gap options, have discontinuous payoffs. For example, suppose a cash-or-nothing call pays off USD 100,000 if the price of a stock at a certain time is above USD 29. If the price is USD 28.9, there is zero payoff; if it is USD 29.1, the payoff is USD 100,000. As a result, traders may have an incentive to engage in illegal price manipulation (especially if the underlying asset is thinly traded).

Lookback Options

• The payoff from a lookback option depends on the maximum or minimum asset price reached during the life of the option. There are four types of lookback options.

1. Floating lookback call – This gives a payoff equal to the amount by which the final asset price exceeds the minimum asset price.
2. Floating lookback put – This gives a payoff equal to the amount by which the maximum asset price exceeds the final asset price.
3. Fixed lookback call – This gives a payoff equal to , where is the maximum asset price in a given time frame and K is the strike price.
4. Fixed lookback put – This gives a payoff equal to , where is the minimum asset price in a given time frame and K is the strike price.

• Lookback options are more expensive than regular options. The value of a lookback option depends on how often the price of the underlying asset is observed. (These observations are used to calculate the maximum or minimum price.) Specifically, a lookback option increases in value as the observation frequency is increased.

Asian Options

• Asian options provide a payoff dependent on an arithmetic average of the underlying asset price during the life of the option. The average price is usually calculated using periodic observations (e.g., at the end of each day).
• Suppose K is the strike price, is the final asset price, and is the average asset price. There are four types of Asian options:

1. Average price calls – Payoff at maturity is equal to .
2. Average price puts – Payoff at maturity equal to .
3. Average strike calls – Payoff at maturity equal to
4. Average strike puts – Payoff at maturity equal to .

• An Asian option is less expensive than a regular option with the same strike price and can be more appropriate for hedging. Consider a company that repatriates its earnings in a foreign currency every week. So its yearly profits depend on the average exchange rate during the year. An Asian put option on the value of the foreign currency can ensure that the average exchange rate will not be worse than a particular exchange rate (i.e., K). This strategy is much less expensive than entering into 52 plain vanilla options (i.e., one option for every week of the year).

Asset Exchange Options

• In an asset-exchange option, the holder has the right to exchange one asset for another. Asset-exchange options can arise in several ways. From the perspective of a US investor, an option to exchange X euros for Y Australian dollars is an option to exchange one asset for another. An offer by Company X to acquire Company Y through the exchange of a certain number of its own shares for shares of Company Y is another type of asset-exchange option.
• Asset-exchange options are closely related to options where a trader will receive the more valuable of two assets (i.e., Asset A and Asset B). This is because the trader’s position can be regarded as a position in Asset A combined with an option to exchange Asset A for Asset B. Similarly, it can be regarded as a position in Asset B combined with an option to exchange Asset B for Asset A.

Basket Options

• A basket option is an option on a portfolio of assets. These portfolios can contain assets such as stocks, stock indices, and currencies. Basket options can be appropriate hedging instruments for firms seeking to reduce costs by hedging their aggregate exposure to several assets with a single trade.
• Basket options are dependent on the correlation between the returns from the assets in the basket. For example, a call option on the future value of a portfolio consisting of ten assets with highly correlated returns is more expensive than a similar call option where the asset returns are uncorrelated (due to portfolio diversification effects).

Volatility Swap

• A volatility swap is appropriate for a trader who wants to take a position dependent only on volatility. While plain vanilla options provide an exposure to volatility, they also depend on the price of the underlying asset. A potential advantage of volatility swaps is that their payoffs depend solely on realized volatility.
• A volatility swap is a forward contract on the realized volatility of an asset during a certain period. A trader agrees to exchange a pre-specified volatility for the realized volatility at the end of the period (with both being multiplied by a certain amount of principal).
• Suppose that is the principal, is the pre-specified yearly volatility, and is the realized yearly volatility (calculated as described above). A swap where the trader pays fixed provides a payoff at the end of the period equal to:

Similarly, a volatility swap where the trader receives fixed provides a payoff at the end of the period equal to:

which is negative of the payoff from the pay-fixed volatility swap.

Volatility Swap – Example

• Suppose that for a pay-fixed volatility swap on the S&P 500 over a three month period –
  • principal, = USD 1 million
  • pre-specified yearly volatility = 15%
  • realized daily volatility, = 1%
  • Find the payoff from this swap and also from corresponding payoff receive-fixed volatility swap.
• Solution –

The payoff from this volatility swap would then be

The corresponding payoff from a receive-fixed volatility swap is equal to -8,700 USD.

Variance Swap

• The payoff from a variance swap is calculated analogously to the payoff from a volatility swap. As a reminder, the variance rate for an asset is the square of its volatility. Thus, the payoff for a pay-fixed variance swap is

where is the principal for the variance swap and V_K is the specified fixed variance. The payoff for a receive-fixed variance swap is similarly:

Sometimes and are specified in a variance swap with the understanding that

Hedging Exotics

• Compared to regular options, some exotics are easier to hedge, while some are more difficult.
  • For example, an average price option is easier to hedge than a regular option because as its maturity approaches, more of the asset prices used to calculate S_ave are observed and thus the payoff becomes progressively more certain. The value of the option therefore has very little sensitivity to asset price movements occurring late in its life.
  • By contrast, barrier options can be quite difficult to hedge because when the asset price is close to the barrier, uncertainty about the payoff increases.

• To deal with difficulties in hedging, traders have developed a hedging procedure known as static options replication. The key principle is that two portfolios that are worth the same on some boundary (which is a function of asset price and time) must also be worth the same at all interior points (i.e., points that could be reached before the boundary is reached). Hence, if a portfolio of plain vanilla options can be found which is worth approximately the same as an exotic option on a boundary, the exotic option can be hedged by shorting the portfolio.
• To illustrate the nature of static options replication, consider a one-year up-and-out call option. The strike price is USD 30, the barrier is USD 50, and the current stock price is USD 25. The natural boundary to use is the one shown in this figure.

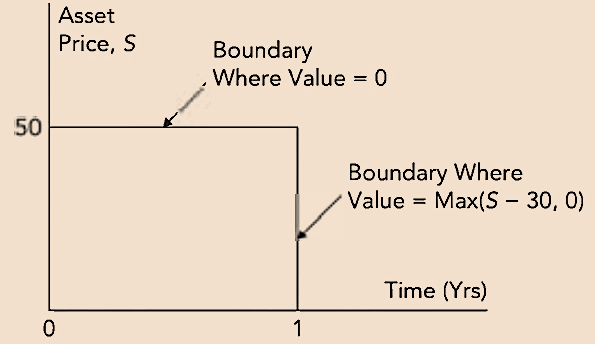
• The up-and-out option is worth zero if the horizontal boundary is reached and max(S-30, 0) if the vertical boundary is reached. The task in static options replication is to choose a portfolio of plain vanilla options that match the payoff as closely as possible on the boundary. The natural first option to use is a one-year European call option with a strike price of 30. This matches the payoff on the vertical part of the barrier. To match payoffs on the horizontal part of the barrier, choose N equally spaced points on the horizontal barrier and an additional N European options with a maturity of less than one year and value each option. Then, solve a set of simultaneous equations to ensure that the portfolio formed from the all the options has a value of zero at each of the N points on the horizontal boundary. As N is increased, the horizontal boundary is matched more precisely and the hedge created by shorting the portfolio improves.
• A static options replication hedge can be left unchanged until the boundary is reached. The trader must then unwind the hedge portfolio and create a new hedge.